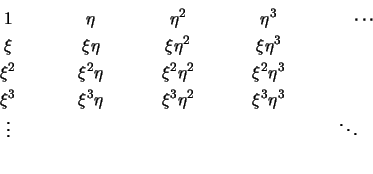 |
(4) |
Bei der Verwendung der Methode der Finiten Elemente ist, wie oben beschrieben, eine Diskretisierung der Geometrie notwendig. Diese Diskretisierung geschieht durch eine Zerlegung in kleine, der mechanischen Theorie genügenden Elemente.
In Abschnitt 2.2.1 wurden die zu lösenden Flächen- und Randintegrale beschrieben. Diese Integrale werden elementweise gelöst. Hierfür ist eine Interpolationsfunktion innerhalb der Elemente notwendig. Als Interpolationsfunktionen werden häufig Polynome verwendet.
Das Pascalsche Polynomschema ist ein einfaches Hilfsmittel zur Auswahl der notwendigen Polynomterme.
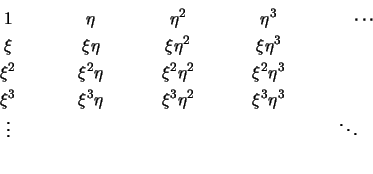 |
(4) |
Für eindimensionale Elemente kann die ersten Spalte oder Zeile des Polynomschemas als Ansatz verwendet werden. Bei zweidimensionalen Elementen sind zur Interpolation zwei Variablen notwendig. Für rechteckige Elemente ist die Auswahl eines rechteckigen Abschnitts, für dreieckige Elemente die Auswahl eines dreieckigen Abschnitts des Polynomschemas notwendig. Untere Polynomglieder dürfen hierbei nicht weggelassen werden.
Als Beispiel ist hier das Polynom für ein Dreieckelemente mit sechs Knoten angegeben. Zur Beschreibung des Elementes sind sechs Polynomterme notwendig, weshalb die quadratischen Anteile mitgenommen werden müssen:
Die Auswahl der verwendeten Polynomterme hängt von verschiedenen Anforderungen ab [Meißner und Menzel 1989]:
Die Diskretisierung selbst erzeugt durch die verwendeten Ansatzfunktionen einen Approximationsfehler. Der Approximationsfehler ergibt sich entsprechend der Taylorreihe aus den abgeschnittenen Gliedern des Terms. Für ein eindimensionales Element sieht das Polynom folgendermaßen aus:
Bei der Auswahl von nur vier Polynomgliedern (kubischer Ansatz) würde das Polynom an der gestrichelten Linie abgeschnitten. Den Approximationsfehler erhält man aus dem abgeschnittenen Teil des Polynoms und ist in diesem Fall vom Grad ![]() .
.