 |
Die Advancing-Front-Methode eignet sich sowohl zur Vernetzung von zweidimensionalen als auch zur Vernetzung von dreidimensionalen Geometrien [Schöberl 1997]. Lokale Verfeinerungen des Netzes sind einfach möglich. Im ebenen Fall können sowohl Dreieckelemente als auch Viereckelemente erzeugt werden. Die Advancing-Front-Methode zur Generierung von Viereckelementen wird Paving-Algorithmus genannt. Tetraederelemente können zur Vernetzung dreidimensionaler Gebilde verwendet werden, für Hexaederelemente scheitert zur Zeit das Verfahren häufig beim Vernähen der Restgeometrie [Schneiders 1996a].
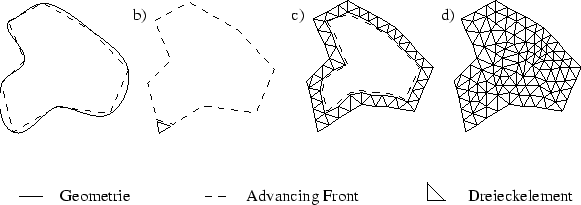
Die Geometrie wird in einem initialen Schritt entsprechend der Dichtefunktion zur Beschreibung der angestrebten Elementkantenlänge diskretisiert (Abbildung 3.2 a)). Die diskretisierte Geometrie stellt die initiale Front dar. Im zweidimensionalen Fall besteht diese initiale Front aus einem Polygonzug, im dreidimensionalen Fall bei der Generierung von Tetraedern aus einem Dreiecknetz und bei der Generierung von Hexaedern aus einem Vierecknetz.
Die Elemente werden im nächsten Schritt der Generierung entsprechend Abbildung 3.2 b) und c) entlang der Front so eingefügt, dass mindestens eine Kante des Elementes auf der Front liegt. Anschließend wird die Front um das neu entstandene Element herum verschoben. Dieser Vorgang wird solange wiederholt, bis die Front nicht mehr vorhanden ist (Abbildung 3.2 d)). Abhängig von der Ausgangsgeometrie können mehrere Fronten vorhanden sein oder zwischenzeitlich entstehen.
Die Advancing-Front-Methode liefert automatisch geglättete Netze. Manuelle Eingriffe zur Steuerung des Algorithmus sind nicht notwendig. Um das Überschneiden von verschiedenen Fronten oder Frontteilen zu vermeiden, ist eine sehr komplexe Suche von Elementen und Knoten in der Nähe der Front nötig. Dadurch ist der Algorithmus sehr langsam.
Bei einer falsch vorgegebenen Dichtefunktion mit zu großen Gradienten kann es möglich sein, dass der Algorithmus scheitert und kein Netz erzeugen kann. Bei der Generierung von Viereckelementen weist der Algorithmus Vorteile gegenüber anderen Verfahren auf. Die Qualität der Netze ist gut und die Anzahl der erzeugten Elemente relativ gering. Irreguläre Punkte, Netzpunkte mit einer von vier abweichenden Anzahl von angrenzenden Elementen (siehe Abschnitt 3.2.2.1), liegen nur im Inneren des Gebietes. Eine Glättung zur Reduzierung der Wirkung der Irregularität ist hierbei möglich.
In der Literatur sind auch Lösungsansätze zur Generierung von Hexaedernetzen mit der Advancing-Front-Methode beschrieben. Diese gehen von einem initialen Vierecknetz auf der Oberfläche der Geometrie aus. Im Inneren der Geometrie bleiben meistens Polyeder übrig, die sich nicht zu Hexaedern vernetzen lassen. Als einfachstes Beispiel hierfür wird unter anderem in [Schneiders 1996a] die Pyramide aus Abbildung 3.3 beschrieben. Das Oberflächennetz aus Vierecken lässt sich beweisbar nicht zu Hexaedern vernetzen.