Generierung von Viereckelementen

Abbildung 3.13: a) lokale Koordinaten, b) Überlappung der lokalen Koordinaten eines Viereckelementes mit einem Innenwinkel größer 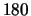$180$ $^{^{\tt \circ}}$

$\parbox{5cm}{a)}$ $\parbox{5cm}{b)}$

$\parbox{5cm}{\psfig{figure=vierecke/viereck_richtig.ps}}$ $\parbox{5cm}{\psfig{figure=vierecke/viereck_falsch.ps}}$

Die Generierung von Netzen aus Viereckelementen ist schwieriger als die Generierung von reinen Dreiecknetzen. Die Ursachen der Schwierigkeiten liegen an Gegebenheiten der Viereckelemente bzw. der Viereckelementnetze:

Ungültige Elementform:

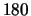
Viereckelemente dürfen nicht jede beliebige Form annehmen. So sind Innenwinkel größer oder gleich 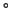$180$ $^{^{\tt\circ}}$unzulässig, da hierbei ein lokales Koordinatensystem nicht mehr eindeutig bestimmbar ist bzw. die lokalen Koordinatenlinien außerhalb des Elementes, wie in Abbildung 3.13 b) dargestellt, liegen. Bei Dreiecken tritt diese Problematik nicht auf, da Dreiecke nur mit Innenwinkeln kleiner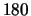 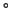$180$ $^{^{\tt\circ}}$erzeugbar sind.

Vernetzbarkeit:

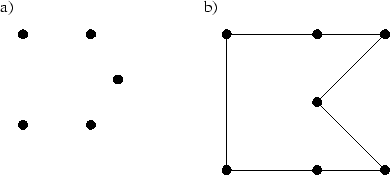
Nicht jede vorgegebene Punktmenge bzw. vorgegebener Polygonzug ist ohne Einfügen von Punkten mit Vierecken vernetzbar. In Abbildung 3.14 sind Beispiele für beide Fälle gegeben. Beliebige Punktmengen oder Randpolygone lassen sich mit gültigen Dreiecken immer vernetzen.

Abbildung 3.14: a) nicht vernetzbare Punktmenge b) nicht vernetzbarer Polygonzug

Die beiden dargestellten Gegebenheiten verursachen weitere ungünstige Einschränkungen bei der Vernetzung mit Viereckelementen:

Teilen einer Kante

Das nachträgliche Teilen einer Kante in zwei Teilkanten ist nicht ohne weiteres möglich, da hierbei nicht vernetzbare Gebiete entstehen können (Abbildung 3.15 a)).

Einfügen einzelner Punkte

Einzelne Punkte können nicht in das Netz eingefügt werden (Abbildung 3.15 b)).

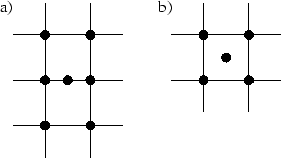
Abbildung 3.15: a) Teilen einer Kante b) Einbau eines Punktes